0. 불균형 데이터(imbalanced data)
- 특정 레이블의 값이 다른 레이블에 비해 과도하게 많은 데이터
- 예 : 암환자(minor)와 일반인(major) / 카드 거래에서 정상거래(major)와 이상거래(minor)
-> minor를 major로 잘못 판단했을 때의 영향이 major를 minor로 잘못 판단했을 때의 영향보다 훨씬 크다.
그래서 minor class에 대한 예측을 높이기 위해 불균형데이터에 처리가 필요함.
방법은 크게 표준화(StandardScaler), 로그변환, 이상치 제거, SMOTE 알고리즘의 4가지.
- 내용 정리에 사용할 데이터 : kaggle 카드거래 데이터
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
card_df = pd.read_csv('./creditcard.csv')
card_df
card_df['Class'].value_counts()0 284315
1 492
Name: Class, dtype: int640은 정상거래, 1은 이상거래. 데이터의 비중이 아주 크게 차이나는 것을 알 수 있다.
이 경우 모델이 major class인 0으로 예측을 전부 해버려도 정확도나 정밀도(precision)등은 90퍼는 쉽게 넘어버리지만, 가장 중요한 것은 minor class를 잘 분류해내는 것인데 그걸 잘 못하는게 문제이다.
전처리를 하고, 학습 데이터와 평가 데이터로 나누어 준 후 Imbalaned Ratio(IR)를 구해보면 매우 큰 것을 확인 가능.
from sklearn.model_selection import train_test_split
def get_preprocessed_df(df=None):
df_copy = df.copy()
df_copy.drop('Time', axis = 1, inplace = True)
return df_copy
def get_train_test_dataset(df=None):
df_copy = get_preprocessed_df(df)
X_features = df_copy.iloc[:,:-1]
y_target = df_copy.iloc[:,-1]
X_train, X_test, y_train, y_test = train_test_split(X_features, y_target, test_size = 0.3, random_state = 0, stratify = y_target)
return X_train, X_test, y_train, y_test
X_train, X_test, y_train, y_test = get_train_test_dataset(card_df)
print('학습 데이터 레이블 값 비율 : ')
print(y_train.value_counts()/y_train.shape[0]*100)
print('테스트 데이터 레이블 값 비율')
print(y_test.value_counts()/y_test.shape[0]*100)학습 데이터 레이블 값 비율 :
0 99.827451
1 0.172549
Name: Class, dtype: float64
테스트 데이터 레이블 값 비율
0 99.826785
1 0.173215
Name: Class, dtype: float64- 모델 구축하고, 학습하고, 예측하고, 평가지표 반환하는 과정
'''
로지스틱 회귀를 통해 분류
'''
from sklearn.linear_model import LogisticRegression
lr_clf=LogisticRegression()
lr_clf.fit(X_train, y_train)
lr_pred = lr_clf.predict(X_test)
lr_pred_proba = lr_clf.predict_proba(X_test)[:,1]
'''
평가지표를 반환하는 함수
'''
from sklearn.metrics import accuracy_score, precision_score, recall_score, confusion_matrix, f1_score, roc_auc_score
def get_clf_eval(y_test, pred=None, pred_proba = None):
confusion = confusion_matrix(y_test, pred)
accuracy = accuracy_score(y_test, pred)
precision=precision_score(y_test, pred)
recall=recall_score(y_test, pred)
f1=f1_score(y_test, pred)
roc_auc = roc_auc_score(y_test, pred_proba)
print('오차 행렬')
print(confusion)
print('정확도 : {0:.4f}, 정밀도 : {1:.4f}, 재현율 : {2:.4f}, F1: {3:.4f}, AUC: {4:.4f}'.format(accuracy, precision, recall, f1, roc_auc))
'''
모델 학습 후 예측을 하고, 앞서 만든 함수를 통해 평가 지표를 반환하는 함수
'''
def get_model_train_eval(model, ftr_train = None, ftr_test = None, tgt_train = None, tgt_test= None):
model.fit(ftr_train, tgt_train)
pred=model.predict(ftr_test)
pred_proba = model.predict_proba(ftr_test)[:,1]
get_clf_eval(tgt_test, pred, pred_proba)
'''
같은 과정을 LightGBM Classifier로도 진행
'''
from lightgbm import LGBMClassifier
lgbm_clf = LGBMClassifier(n_estimators = 1000, num_leaves = 64, n_jobs =-1, boost_from_average = False)
모델의 성능을 비교해보면,
get_model_train_eval(lgbm_clf, ftr_train = X_train, ftr_test= X_test, tgt_train=y_train, tgt_test=y_test)
get_clf_eval(y_test, lr_pred, lr_pred_proba)# LGBMClassifier의 성능
오차 행렬
[[85290 5]
[ 36 112]]
정확도 : 0.9995, 정밀도 : 0.9573, 재현율 : 0.7568, F1: 0.8453, AUC: 0.9790
# LogisticRegression의 성능
오차 행렬
[[85282 13]
[ 61 87]]
정확도 : 0.9991, 정밀도 : 0.8700, 재현율 : 0.5878, F1: 0.7016, AUC: 0.9600정확도가 매우 높은데, 이건 모델이 전부 major로 예측해버려도 나올 수 있는 수치이다.
minor를 major로 판단하는 것에 대한 지표인 재현율을 보면, 각각 0.75와 0.58로 다른 지표들에 비해 현저히 낮은 것을 확인할 수 있는데, 이는 극히 적은 수의 minor 클래스를 제대로 분류하지 못했기 때문이다.
이제 여러 과정을 거쳐 불균형 데이터에 대해서도 분류의 성능을 높일 수 있는 방법을 정리한다.
1. 표준화(StandardScaler)
import seaborn as sns
plt.figure(figsize=(8,4))
plt.xticks(range(0, 30000, 1000), rotation = 60)
sns.distplot(card_df['Amount'])데이터의 여러 피처 중 'Amount'는 정상거래와 사기거래를 결정하는 매우 중요한 속성이다. 이 데이터 피처를 시각화해보면,
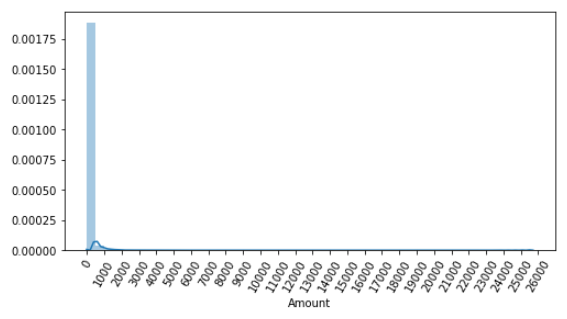
데이터의 분포가 왼쪽으로 매우 치우친(skewed) 것을 알 수 있다.
예측의 성능을 높이기 위해 0과 1사이의 값으로 변환해주는 StandardScaler()를 적용한 후, 다시 모델의 성능을 측정해본다.
from sklearn.preprocessing import StandardScaler
def get_preprocessed_df(df=None):
df_copy = df.copy()
scaler = StandardScaler()
amount_n = scaler.fit_transform(df_copy['Amount'].values.reshape(-1,1))
df_copy.insert(0, 'Amount_scaled', amount_n)
df_copy.drop(['Amount', 'Time'], axis = 1, inplace = True)
return df_copy
X_train, X_test, y_train, y_test = get_train_test_dataset(card_df)
lr_clf = LogisticRegression()
get_model_train_eval(lr_clf, ftr_train = X_train, ftr_test = X_test, tgt_train = y_train, tgt_test = y_test)
print("### LGBM 예측 성능 ###")
lgbm_clf = LGBMClassifier(n_estimators = 1000, num_leaves = 64, n_jobs = -1, boost_from_average = False)
get_model_train_eval(lgbm_clf, ftr_train = X_train, ftr_test = X_test, tgt_train = y_train, tgt_test = y_test)### 로지스틱 회귀의 성능 지표 ###
오차 행렬
[[85281 14]
[ 58 90]]
정확도 : 0.9992, 정밀도 : 0.8654, 재현율 : 0.6081, F1: 0.7143, AUC: 0.9702
### LGBM 예측 성능 ###
오차 행렬
[[85290 5]
[ 37 111]]
정확도 : 0.9995, 정밀도 : 0.9569, 재현율 : 0.7500, F1: 0.8409, AUC: 0.9779앞의 경우보다는 재현율이 많이 개선되었지만, 그래도 다른 지표에 비해서는 비교적 낮다.
2. 로그 변환
- 데이터의 분포가 심하게 왜곡되어있을 때(skewed) 사용할 수 있는 기법이고,
- 원래 값을 log값으로 전환하여 값을 줄이게 되는데 이런 특징때문에 데이터 피처 간의 단위가 크게 차이나는 경우에도 사용할 수 있다.
def get_preprocessed_df(df=None):
df_copy = df.copy()
amount_n = np.log1p(df_copy['Amount']) # 로그 변환하는 코드 추가
df_copy.insert(0, 'Amount_scaled', amount_n)
df_copy.drop(['Amount', 'Time'], axis = 1, inplace = True)
return df_copyX_train, X_test, y_train, y_test = get_train_test_dataset(card_df)
print('로지스틱 회귀 예측 성능 ')
get_model_train_eval(lr_clf, ftr_train= X_train , ftr_test = X_test, tgt_train = y_train, tgt_test = y_test)
print('LIGHTGBM 예측 성능')
get_model_train_eval(lgbm_clf, ftr_train = X_train, ftr_test = X_test, tgt_train = y_train, tgt_test = y_test)로지스틱 회귀 예측 성능
오차 행렬
[[85283 12]
[ 59 89]]
정확도 : 0.9992, 정밀도 : 0.8812, 재현율 : 0.6014, F1: 0.7149, AUC: 0.9727
LIGHTGBM 예측 성능
오차 행렬
[[85290 5]
[ 35 113]]
정확도 : 0.9995, 정밀도 : 0.9576, 재현율 : 0.7635, F1: 0.8496, AUC: 0.9796- 이 경우 오히려 로지스틱 회귀는 표준화를 거쳤을 때보다 재현율이 더 낮아졌다.
3. 이상치 제거
이 지점에서 많은 회의감이 들었다.. 이전에 교수님이 왜 그런 말을 하셨는지 다시금 곱씹게 됨

25%, 75%까지의 범위 밖으로 일정 구간을 더 해 정상이라 볼 수 있는 구간을 정의하고, 그 구간 바깥의 값은 이상치로 정의한 후 데이터세트에서 빼버리는 방법.
- 이상치를 구하기 위한 IQR(Interquatile Range)를 정의하고, 구간 밖에 있는 데이터를 찾아내 인덱스를 반환하는 함수
def get_outlier(df=None, columns = None, weight = 1.5):
fraud = df[df['Class']==1][columns]
quantile_25 = np.percentile(fraud.values, 25)
quantile_75 = np.percentile(fraud.values, 75)
iqr = quantile_75-quantile_25
iqr_weight = iqr*weight
lowest_val = quantile_25-iqr_weight
highest_val = quantile_75+iqr_weight
outlier_index = fraud[(fraud<lowest_val)|(fraud>highest_val)].index
return outlier_index정의한 함수로 이상치의 인덱스를 반환해보면 아래와 같다.
outlier_index = get_outlier(df=card_df, columns = 'V14', weight = 1.5)
print('이상치 데이터 인덱스 : ', outlier_index)이상치 데이터 인덱스 : Int64Index([8296, 8615, 9035, 9252], dtype='int64')그 뒤 전처리 함수에 이상치를 제거하는 부분을 추가한 후, 적용하여 모델의 성능을 다시 평가해본다.
def get_preprocessed_df(df=None):
df_copy = df.copy()
amount_n = np.log1p(df_copy['Amount'])
df_copy.insert(0, 'Amount_scaled', amount_n)
df_copy.drop(['Amount', 'Time'], axis = 1, inplace=True)
outlier_index = get_outlier(df=df_copy, columns = 'V14', weight = 1.5)
df_copy.drop(outlier_index, axis = 0, inplace=True) # 이상치 제거
return df_copy성능 평가 결과
X_train, X_test, y_train, y_test = get_train_test_dataset(card_df)
print("#### 로지스틱 회귀 예측 성능 ####")
get_model_train_eval(lr_clf, ftr_train = X_train, ftr_test = X_test, tgt_train = y_train, tgt_test = y_test)
print("#### LIGHTGBM 예측 성능 ####")
get_model_train_eval(lgbm_clf, ftr_train = X_train, ftr_test = X_test, tgt_train = y_train, tgt_test = y_test)#### 로지스틱 회귀 예측 성능 ####
오차 행렬
[[85281 14]
[ 48 98]]
정확도 : 0.9993, 정밀도 : 0.8750, 재현율 : 0.6712, F1: 0.7597, AUC: 0.9743
#### LIGHTGBM 예측 성능 ####
오차 행렬
[[85290 5]
[ 25 121]]
정확도 : 0.9996, 정밀도 : 0.9603, 재현율 : 0.8288, F1: 0.8897, AUC: 0.9780LGBM의 경우 재현율이 계속 높아지고 있는데 로지스틱 회귀는 성능이 더 떨어졌다.
지금까지의 결과로 봐선 불균형 데이터셋일 때 로지스틱 함수는 쓰면 안되지 싶다.
4. SMOTE
pip install -U imbalanced-learn ### 왜 conda 설치는 매번 실패하지from imblearn.over_sampling import SMOTE
smote = SMOTE(random_state = 0)
X_train_over, y_train_over = smote.fit_sample(X_train, y_train)
print('SMOTE 적용 전 학습용 피처/레이블 데이터 세트 : ', X_train.shape, y_train.shape)
print('SMOTE 적용 후 학습용 피처/레이블 데이터 세트 : ', X_train_over.shape, y_train_over.shape)
print('SMOTE 적용 후 레이블 값 분포 : \n', pd.Series(y_train_over).value_counts())SMOTE 적용 전 학습용 피처/레이블 데이터 세트 : (199362, 29) (199362,)
SMOTE 적용 후 학습용 피처/레이블 데이터 세트 : (398040, 29) (398040,)
SMOTE 적용 후 레이블 값 분포 :
1 199020
0 199020
Name: Class, dtype: int64- 오버샘플링된 것을 확인할 수 있다.
그럼 로지스틱의 성능을 다시 평가해보면,
lr_clf = LogisticRegression()
get_model_train_eval(lr_clf, ftr_train = X_train_over, ftr_test = X_test, tgt_train =y_train_over, tgt_test= y_test)오차 행렬
[[82937 2358]
[ 11 135]]
정확도 : 0.9723, 정밀도 : 0.0542, 재현율 : 0.9247, F1: 0.1023, AUC: 0.9737재현율은 엄청나게 높아졌는데, 정밀도가 엄청나게 떨어졌다.
오버샘플링된 데이터로 인해 Class = 1인 데이터를 너무 많이 학습했고, 그러다보니 Class = 0도 Class = 1로 예측하는 경우가 너무 많이 생겨서 발생한 일이다.
모델의 문제점을 찾기 위해 로지스틱 함수의 재현율과 정밀도 그래프를 그려보면,
from sklearn.preprocessing import Binarizer
from sklearn.metrics import precision_recall_curve
def precision_recall_curve_plot(y_test, pred_proba):
precisions, recalls, thresholds = precision_recall_curve(y_test, pred_proba)
plt.figure(figsize = (8,6))
threshold_boundary = thresholds.shape[0]
plt.plot(thresholds, precisions[0:threshold_boundary], linestyle = '-', label = 'precision')
plt.plot(thresholds, recalls[0:threshold_boundary], label = 'recall')
start, end = plt.xlim()
plt.xticks(np.round(np.arange(start, end, 0.1), 2))
plt.xlabel('Treshold value '); plt.ylabel('Precision and Recall Value')
plt.legend();plt.grid()
plt.show()
precision_recall_curve_plot(y_test, lr_clf.predict_proba(X_test)[:,1])
두 값이 같이 높아지는 지점은 없고, 마치 둘 사이에 trade-off가 있는 것 같은 관계가 보인다. (실제로는 상관 無)
==> 결국 이럴 땐 로지스틱은 쓰지 않는 것이 맞는 것 같다.
오버샘플링된 데이터로 LGBM으로 예측을 수행해보면,
lgbm_clf = LGBMClassifier(n_estimators = 1000, num_leaves = 64, n_jobs = -1, boost_from_average = False)
get_model_train_eval(lgbm_clf, ftr_train = X_train_over, ftr_test = X_test, tgt_train = y_train_over, tgt_test = y_test)
###오버샘플링은 학습데이터에만오차 행렬
[[85283 12]
[ 22 124]]
정확도 : 0.9996, 정밀도 : 0.9118, 재현율 : 0.8493, F1: 0.8794, AUC: 0.9814모든 지표가 아무런 처리를 하지 않았을 때보다 상당히 향상되었음을 확인할 수 있다.
그럼 어떤 원리로 오버샘플링이 진행되는 것이냐
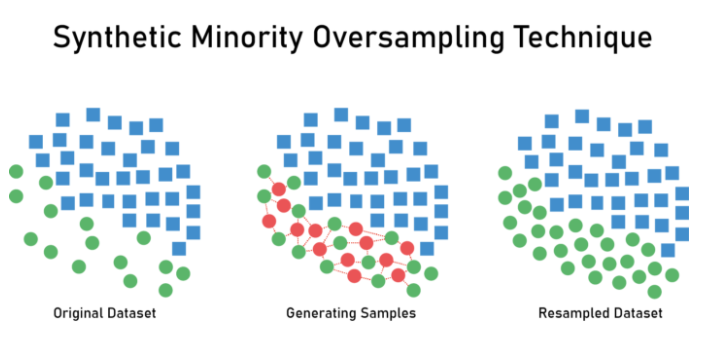
minor class에서 각각의 샘플들의 K-neighbors를 찾고, 각각의 군집들을 선으로 이은 후 선 위에 랜덤으로 새로운 minor class를 생성하여 데이터의 비율을 어느 정도 맞추는 기법이다.
(가운데 그림의 빨간색이 SMOTE를 통해 임의로 생성된 인위적 샘플)
이외에도 BLSMOTE(Border Line SMOTE) - minor class와 major class를 나누는 경계를 찾고, 그 경계선 위에 minor를 증폭시켜 주는 오버샘플링 기법이 있음.
또는 major의 수를 줄이는 언더샘플링(under sampling)도 가능은 한데, 구태여 정보를 줄일 필요는 없다 생각.
* Tomek Links :
서로 다른 클래스의 데이터를 모두 이은 후, 가장 짧은 거리로 묶인 점들의 조합(Tomek Link)을 찾는다
Tomek Link에서 Major 클래스만 지워주는 방식으로 언더 샘플링이 진행된다.
- 또는 Easy Ensemble, Balance Cascade 등등이 존재.
5. 오버샘플링 vs. 언더샘플링
- Over sampling
* 데이터를 늘리기에 시간이 오래걸리고, 과하게 생성될 수 있고 과적합 문제가 발생할 수 있음
* 오버샘플링때문에 두 클래스를 구분짓는 의사결정경계가 과하게 커질 수 있고, 기존의 데이터 분포와는 달라질 수 있음.
==> 이런 문제때문에 현재에는 hybird resampling기법(ex. DBSM)같은 것들이 개발
- Under sampling
* 학습에 필요하지 않은 데이터의 수를 줄여서 학습속도는 높아지지만,
* 의사결정경계에 있는 데이터를 삭제하게 되는 경우 학습에 악영향을 미친다.
==> 학습속도향상의 이점보다 잃는 것이 많기 때문에 안하는게 좋아보인다.
이번 주차의 다른 내용인 스태킹 앙상블 모델과, AutoML은 다른 글로 정리해야겠음 내용 너무 많음.
출처 :
Interquartile Range (IQR) to Detect Outliers | Naysan Saran
Interquartile Range (IQR) to Detect Outliers | Naysan Saran
According to Investopedia, Per capita GDP is a global measure for gauging the prosperity of nations and is used by economists, along with GDP, to analyze the prosperity of a country based on its economic growth.
naysan.ca
SMOTE로 데이터 불균형 해결하기. 현실 세계의 데이터는 생각보다 이상적이지 않다. | by John | Medium
SMOTE로 데이터 불균형 해결하기
현실 세계의 데이터는 생각보다 이상적이지 않다.
john-analyst.medium.com
'통계학 > BITAmin' 카테고리의 다른 글
| unicodedecodeerror: 'utf-8' codec can't decode byte 0xc3 in position 9382: invalid continuation byte (오류해결?) (0) | 2021.07.18 |
|---|---|
| 12주차 : 2학기 기말고사, 복습과제로 오답정리 (0) | 2021.01.12 |
| 11주차 : Bagging, Boosting - AdaBoost, GBM, XGBoost, LightGBM (0) | 2021.01.04 |
| 10주차 복습 : KNN, SVM, Ensemble (0) | 2020.12.11 |




댓글