4 ~ 5주차 : Volatility Clustering, ARCH, GARCH

0. 들어가기

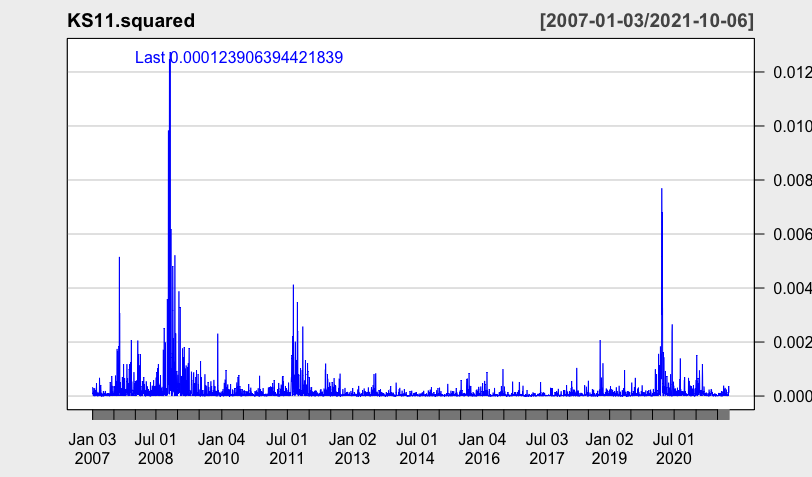
- 주가 종합 지수인 KOSPI 시계열의 daily return을 제곱해서 변동성의 추이를 살펴보면, 변동성이 큰 시기와 작은 시기가 군집을 이루어 존재하는 것을 확인할 수 있음.

- 이처럼 금융 수익률 데이터에서는 변동성 군집(volatility clustering) 현상이 흔히 나타나곤 하는데, 변동성을 예측할 수 있는 ARCH모형과 더 나아가 GARCH, GARCH의 확장형에 대해 정리하고자 함.

 

squared return 또는 absolute return은 수익률 변동성의 proxy로 널리 쓰인다. 그래프는 quantmod로 그렸음.

1. 변동성이란

- 자산 수익률의 조건부 표준편차(또는 분산)을 의미

$$ \mbox{daily log return} = r_{t} = log(P_{t}/P_{t-1}) $$

$$ \mbox{volatility} = \sigma = \sqrt{Var(r_{t+h}|I_{t})} , I_{t} \mbox{는 t기의 정보집합} $$

 

- 수익률과 변동성의 추정량

$$ 252 \bar{r_{T}} = \mbox{연간 수익률} $$

$$ \sqrt{252s_{T}} = \mbox{변동성의 추정량} $$

* 1년 중 영업일은 평균적으로 252일이기 때문에 252를 추가하여 도출한다고 함.

 

- 직접 관측이 불가하므로, 대용변수를 써서 변동성을 가늠함

 

✨ 주로 사용하는 대용변수들(proxy)

(1) squared returns 

- 수익률을 제곱해서 판단

(2) absolute returns

- 수익률에 절대값을 취해서 변동폭의 추이를 판단

(3) realized variance : "실현된 분산"

- high-frequency data에 적합한 구조를 가지고 있음

- intraday price의 평균값을 통해 계산

 👀 def. realized variance

$$ p_{i,t} = \mbox{log price of asset i at time t} $$

$$ \Delta = \mbox{fraction of a trading session w.r.t the implied sampling frequency} $$

$$ m = \frac{1}{\Delta} = \mbox{the number of sampled observations per trading session} $$

$$ T = \mbox{the number of days in the sample} $$

$$ \mbox{총 관측치 수} = mT $$