New Keynesian model : 명목실효하한과 최적 통화 정책 (~ing)

Werning(2012) : Managing a liquidity trap, MIT working paper

 

[사용할 모델] 뉴케인지언 모형

1. dynamic IS curve : Euler Equation을 로그선형화해서 도출

$$ \dot{x}(t) = \frac{1}{\sigma}[i(t)- {\pi}(t)-r^{n}(t)] $$

2. NKPC(New Keynesian Philips Curve)

$$ \dot{x}(t) = \rho{\pi}(t) - \kappa x(t) $$

k는 가격(물가)이 신축적인 정도를 나타내는 파라미터

3. interest rate rule

$$ i(t) = r^{n}(t) + \phi_{\pi}{\pi}(t) $$

$$\phi_{\pi}\le1 \text{일 때는 multiple equilibria 발생}$$ 

$$\phi_{\pi}>1 \text{일 때는 unique eqbm으로 나타남}$$ 

 

4. 명목 실효 하한(zero lower bound)의 가정

$$ i(t) \ge 0 $$

 

1. 가정

- T기간 동안 경제는 유동성 함정에 빠진다

- 사회후생에 관한 손실함수의 형태

$$ \mathcal{L} = {1 \over 2} \int_{0}^{\infty} e^{-\rho t} (x(t)^{2} + \lambda{\pi}(t)^{2})dt, \lambda \overset{\underset{\mathrm{def}}{}}{=} {\lambda \over \kappa} \ge 0 $$

- 중립금리의 시간경로

 

$$ r^{n} (t) = \underline{r},  \quad\text{if t}  \in [0, T) $$

$$ r^{n} (t) = \bar{r},  \quad\text{if t}  \in [T, \infty) $$ 

- 통화당국은 금리정상화 이후 (t>= T)에는 원래의 sufficiently reactive i-rule에 따라 정책을 운영함

$$ (x(t), \pi(t))  = (0, 0) \quad \forall t \ge T $$이 되도록 운영

이 때, liquidity trap에 빠졌을 때의 동학은 어떨까 ?

 

2. Qualitative Analysis

i. 1st best solution

[가정] 

- 유동성 함정에 빠진 기간 : 

$$ t < T $$

- 0의 명목하한에 도달 :

$$ i(t) =  0 $$

[system of equations]

(1) output gap의 동학

$$ \dot{x(t)} = - \frac {1}{\sigma} (\pi(t) + \underline{r}) $$

(2) inflation의 동학

$$ \dot{\pi(t)} = \rho\pi(t) - \kappa x(t) $$

(3) terminal condition

$$ (x(T) , \pi(T)) = (0, 0) $$

 

[dynamics & phase diagram]

$$ \dot{x(t)} > 0 \Longleftrightarrow \pi(t) < - \underline{r} (>0) $$

$$ \dot{\pi(t)} > 0 \Longleftrightarrow x(t) < \frac {\rho}{\kappa} {\pi(t)} $$

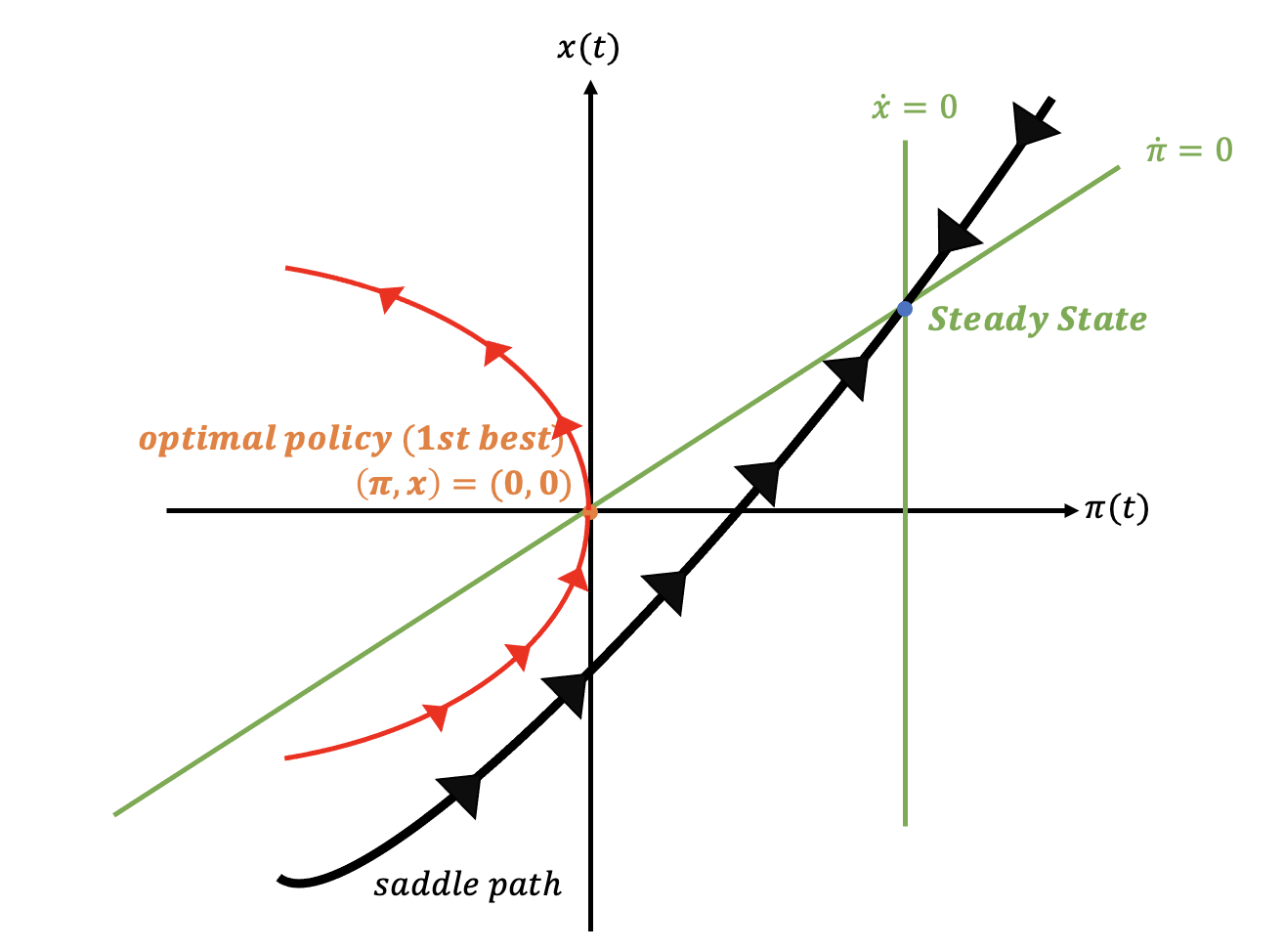
- optimal policy 시행시 

* 디플레이션과 경기침체를 겪다가, 시간이 흐름에 따라 점차 완화되어 말기 조건인 (0, 0)에 도달한다

* 최초 침체의 정도는 유동성 함정에 빠져있는 기간이 길수록 심해진다.

x(0), pi(0)의 위치는 빨간색 경로 상에 위치하는데, 유동성 함정에 빠져있는 기간이 길수록 빨간색 경로의 왼쪽에 위치하고, 경로를 역으로 따라가면 더 깊은 디플레이션과 불황을 나타냄

직관 ) 

$$ i(t) - \pi(t) = - \pi(t) (>0) $$ 실질금리가 이 기간동안 너무 높아서 소비, 투자, 생산 모두 위축시키고,

$$ \pi^{e} (t) $$ 마저도 낮춰버린다.

$$ t \rightarrow \infty $$ 일수록 그 정도는 더욱 심해진다.